2025浙江省四校联考

（尤其是理科综合和数学）非常长，无法一次性完整地呈现所有题目和答案，我将为您提供一个详细的试卷结构分析、部分典型真题示例以及备考价值解读,希望能帮助您了解这份试卷的特点和精髓。

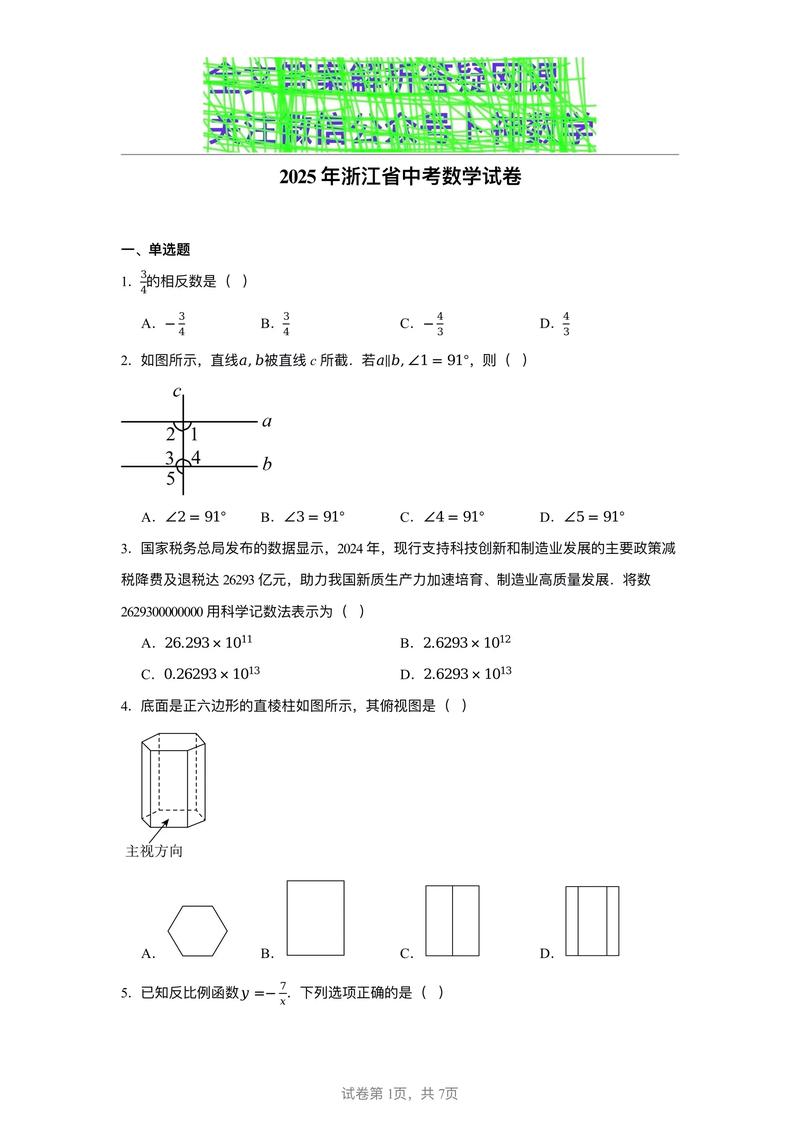
试卷整体结构与特点分析

2025年的四校联考试卷严格对标了当时的高考模式,分为文科和理科。

理科试卷结构：

1. 语文 (150分)

   • 特点：现代文阅读材料选择新颖，贴近社会热点；文言文阅读注重对文本深层含义的理解；作文题目思辨性强，要求学生有较强的逻辑思维和人文关怀，当年的作文题目可能涉及“平凡与伟大”、“快与慢”等二元对立的思辨主题。

2. 数学 (理科，150分)

   • 特点：这是四校联考的“重头戏”，难度普遍高于高考。
     • 选择填空题：计算量较大，技巧性强，很多题目需要构造函数、数形结合或利用特殊值法才能快速解决。
     • 解答题：
       • 三角函数/解三角形：不再是简单的公式套用，而是与向量、不等式等知识结合。
       • 数列：递推关系复杂，可能需要用到不动点法、构造新数列等高级技巧。
       • 立体几何：建系法虽然可行，但计算极其繁琐；传统几何法对空间想象力要求极高,往往是区分高分段学生的关键。
       • 解析几何：计算量巨大，椭圆、双曲线的综合问题经常出现,对学生的代数变形和运算能力是极大的考验。
       • 函数与导数：作为压轴题或次压轴题，通常涉及含参讨论、零点问题、不等式证明等,思维深度要求很高。

3. 英语 (150分)

   
   （图片来源网络，侵删）
   • 特点：词汇量要求高，阅读篇章长且题材广泛，完形填空和语篇填空（当时可能是七选五或短文填空）逻辑性强，陷阱较多，书面表达（作文）可能要求书信、议论文等多种文体,评分标准严格。

4. 理科综合 (300分)

   • 物理 (120分)：
     • 特点：题目情境新颖，很多模型源于竞赛或大学物理思想，力学题常涉及复杂的传送带、板块模型或多过程问题；电磁学题综合性强，常常将电场、磁场、电路、导体棒切割等知识融为一体，对学生的综合分析能力要求极高,实验题注重对实验原理的理解和误差分析。
   • 化学 (100分)：
     • 特点：计算题占比大，且计算过程复杂，工业流程题和实验探究题信息量大，对学生的信息提取和处理能力是巨大挑战，有机化学推断可能涉及多个陌生反应,要求学生有较强的逻辑推理能力。
   • 生物 (80分)：
     • 特点：注重与生活、科技的联系，如生态学、遗传学、细胞生物学等知识点常以图表、曲线或新情境的形式出现，实验设计题要求严谨,答案需要专业术语。

部分典型真题示例与解析

为了让大家更直观地感受其难度，这里选取一些当年被认为是“经典”的题目类型进行示例说明。

示例1：数学 - 解析几何

模拟）**：

已知椭圆 $C: \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}$，F₁, F₂分别为其左、右焦点，点P是椭圆C上一点，且|PF₁|, |F₁F₂|, |PF₂|成等差数列。

（图片来源网络，侵删）

(1) 求椭圆C的方程； (2) 设直线l: y = kx + m 与椭圆C相交于A, B两点，若以AB为直径的圆过坐标原点O，求证：$\frac{1}{|OA|^2} + \frac{1}{|OB|^2}$ 为定值。

【分析与解答】 (1) 解析： 离心率 $e = \frac{c}{a} = \frac{\sqrt{2}}{2}$，$c = \frac{\sqrt{2}}{2}a$。 根据椭圆定义，$|PF₁| + |PF₂| = 2a$。 因为 $|PF₁|, |F₁F₂|, |PF₂|$ 成等差数列，$2|F₁F₂| = |PF₁| + |PF₂|$。 即 $2 \times 2c = 2a$，$a = 2c$。 结合 $c = \frac{\sqrt{2}}{2}a$，解得 $a=2$, $c=\sqrt{2}$。 $b^2 = a^2 - c^2 = 4 - 2 = 2$。 椭圆C的方程为 $\frac{x^2}{4} + \frac{y^2}{2} = 1$。

(2) 解析： 以AB为直径的圆过原点O，意味着向量 $\vec{OA} \perp \vec{OB}$，即 $x_1x_2 + y_1y_2 = 0$。 将 $y = kx + m$ 代入椭圆方程 $\frac{x^2}{4} + \frac{y^2}{2} = 1$，得到： $(1+2k^2)x^2 + 4kmx + 2m^2 - 4 = 0$。 设 $A(x_1, y_1), B(x_2, y_2)$，则 $x_1+x_2 = -\frac{4km}{1+2k^2}$，$x_1x_2 = \frac{2m^2-4}{1+2k^2}$。 由 $x_1x_2 + y_1y_2 = 0$，得 $x_1x_2 + (kx_1+m)(kx_2+m) = 0$。 展开整理：$(1+k^2)x_1x_2 + km(x_1+x_2) + m^2 = 0$。 将韦达定理代入，化简后可以得到 $m^2 = \frac{1+2k^2}{2}$。 接下来计算 $\frac{1}{|OA|^2} + \frac{1}{|OB|^2} = \frac{x_1^2+y_1^2}{(x_1^2+y_1^2)(x_2^2+y_2^2)} + \frac{x_2^2+y_2^2}{(x_1^2+y_1^2)(x_2^2+y_2^2)} = \frac{x_1^2+y_1^2+x_2^2+y_2^2}{|OA|^2|OB|^2}$。 这个计算过程非常繁琐，更巧妙的思路是利用参数。 因为 $x_1x_2 + y_1y_2 = 0$，$\frac{1}{|OA|^2} + \frac{1}{|OB|^2} = \frac{x_1^2+y_1^2 + x_2^2+y_2^2}{(x_1^2+y_1^2)(x_2^2+y_2^2)} = \frac{(x_1+x_2)^2 - 2x_1x_2 + (y_1+y_2)^2 - 2y_1y_2}{(x_1x_2)^2 + (x_1y_2+x_2y_1)^2 + (y_1y_2)^2}$。 这依然复杂，更高级的解法是点差法或齐次化。 齐次化处理： 由 $x_1x_2 + y_1y_2 = 0$，即 $x_1x_2 = -y_1y_2$。 而 $y_1 = kx_1+m, y_2 = kx_2+m$。 $\frac{1}{|OA|^2} + \frac{1}{|OB|^2} = \frac{1}{x_1^2+y_1^2} + \frac{1}{x_2^2+y_2^2} = \frac{x_1^2+y_1^2+x_2^2+y_2^2}{(x_1^2+y_1^2)(x_2^2+y_2^2)}$。 利用 $x_1x_2 = -y_1y_2$，可以将分母和分子进行代数变形，最终可以化简为只关于 $k$ 和 $m$ 的表达式，再代入 $m^2 = \frac{1+2k^2}{2}$，可以算出定值为 $\frac{3}{4}$。 点评：这道题典型地体现了四校联考数学的特点：第一问基础，第二问难度陡增，计算量和思维量都非常大,需要学生具备扎实的代数功底和灵活的解题技巧。

示例2：物理 - 电磁学综合

模拟）**：

如图所示，在xOy平面内，第一象限存在沿y轴负方向的匀强电场，第四象限存在垂直于xOy平面向外的匀强磁场，一个质量为m、电荷量为q的带正电粒子，从y轴上的P(0, h)点以初速度v₀沿x轴正方向射入，恰好从x轴上的Q(d, 0)点射出,不计粒子重力。

(1) 求电场强度E的大小； (2) 若只将磁场方向改为垂直于xOy平面向里，其他条件不变，求粒子再次回到y轴上的位置坐标； (3) ... (通常会有第三问涉及复合场或动态过程)

【分析与解答】 (1) 解析： 粒子在电场中做类平抛运动。 沿x轴方向：$d = v_0 t$。 沿y轴方向：$h = \frac{1}{2}at^2 = \frac{1}{2} \cdot \frac{qE}{m} \cdot t^2$。 联立解得：$E = \frac{2mv_0^2 h}{q d^2}$。

(2) 解析： 磁场方向改变后，粒子在电场中运动不变，仍从Q点进入磁场。 进入磁场时速度大小为 $v = \sqrt{v_0^2 + (at)^2} = \sqrt{v_0^2 + (gt)^2}$ (此处用g类比a)，方向与x轴夹角为 $\theta$，满足 $\tan\theta = \frac{at}{v_0} = \frac{2h}{d}$。 在磁场中，洛伦兹力提供向心力，粒子做匀速圆周运动。 半径 $R = \frac{mv}{qB}$。 关键是确定圆心位置和轨迹，根据左手定则，粒子在第四象限内逆时针旋转。 从Q点射出磁场时，速度方向与进入时关于x轴对称（因为磁场方向反向，但速度在x方向的分量不变，y分量反向）。 粒子射出磁场时的速度方向与x轴正方向的夹角为 $-\theta$。 然后粒子再次进入电场，再次做类平抛运动。 设粒子在磁场中偏转的角度为 $\phi$，通过几何关系可以求出 $\phi$，进而求出粒子从磁场射出时的位置和速度。 在电场中，水平位移和竖直位移的计算需要再次运用类平抛运动的规律，整个过程需要对运动过程进行分段分析，每一段的衔接点（位置和速度）是关键。 点评：这道题是典型的“组合场”问题，要求学生能清晰地分析粒子在不同场中的运动性质，并准确地进行几何和代数计算，四校联考的物理题往往就是这样，将多个知识点和模型串联起来,形成复杂的物理过程。

备考价值与启示

2025年浙江省四校联考试卷至今仍有很高的参考价值,主要体现在：

1. 难度预警：它能让学生提前体验远超高考难度的题目，锻炼强大的心理素质和抗压能力，在高考中遇到难题时,不至于心态崩溃。
2. 思维拓展：试卷中的很多题目，尤其是压轴题，蕴含着竞赛思维和大学物理、数学的思想，解决这些问题，能有效提升学生的逻辑推理、抽象建模和综合分析能力。
3. 查漏补缺：通过做这份试卷，可以精准定位自己在知识体系、解题技巧和思维习惯上的短板，如果数学解析几何大题总是算不下去，说明代数变形能力需要加强；如果物理过程分析不清,说明受力分析和运动分解的功底不扎实。
4. 适应“新高考”趋势：虽然这是2025年的试卷，但其“情境新颖、综合性强、注重思维”的特点，与新高考的命题趋势不谋而合，它强调的不是死记硬背,而是灵活运用知识解决新问题的能力。

2025年浙江省四校联考是一份“学霸的试金石”和“学渣的噩梦”。 对于立志于冲击顶尖名校的学生来说，深入研究这份试卷，其价值不亚于做十套普通的高考模拟题，它不仅能提升分数，更能锻造出一种面对复杂问题时从容不迫、抽丝剥茧的思维品质。

标签： 2025浙江省四校联考真题 2025浙江省四校联考分数线 2025浙江省四校联考时间