2025年两校联考真题难度如何？

99ANYc3cd6 联考资讯 2026-01-16 2

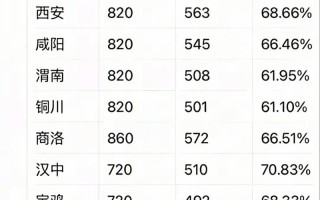
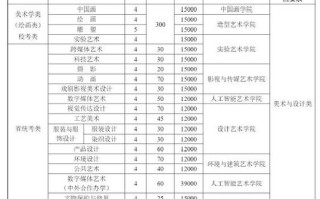
“两校联考”通常指的是清华大学和北京大学在2010-2025年间牵头组织的自主招生联考。 2025年，这两个联盟分别被称为“北约”和“华约”，它们各自包含不同的顶尖高校，考试内容和风格也各有侧重。

（图片来源网络，侵删）

北约联盟（以北京大学为首）：包括北京大学、北京航空航天大学、北京师范大学、复旦大学、哈尔滨工业大学、香港大学、南开大学、清华大学、上海交通大学、厦门大学、四川大学、天津大学、武汉大学、中山大学、中国科学技术大学、浙江大学等16所高校。
华约联盟（以清华大学为首）：包括清华大学、中国人民大学、上海交通大学、南京大学、浙江大学、中国科学技术大学、西安交通大学等7所高校。

2025年是这两个联盟联考的鼎盛时期之一,其试题以难度大、思维灵活、知识面广而著称，对考生的综合能力要求极高，下面我们分别对两个联盟的考试特点和典型真题进行解析。

2025年“北约”联考真题解析

“北约”的考试风格更偏向于基础、灵活和思维深度，强调对学科核心概念的理解和运用，题目往往看似简单，但需要深入的思考和巧妙的解法。

数学部分特点与真题示例

特点：

重视基础概念：题目往往围绕函数、数列、不等式等核心概念展开。
强调思维方法：非常考验数形结合、分类讨论、构造函数等数学思想。
计算量适中，但思维难度大：不需要繁琐的计算，但解题路径可能非常隐蔽。

真题示例1（函数与导数）：设函数 $f(x) = \frac{\ln x}{x}$。

（图片来源网络，侵删）

(1) 求 $f(x)$ 的单调区间； (2) 证明：对任意的 $n \in \mathbb{N}^*$，都有 $\frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n+1} < \ln(n+1) < 1 + \frac{1}{2} + \dots + \frac{1}{n}$。

解析：这道题是典型的“北约”风格。 (1) 问是基础求导，$f'(x) = \frac{1 - \ln x}{x^2}$，易知，当 $0 < x < e$ 时，$f'(x) > 0$，函数单调递增；当 $x > e$ 时，$f'(x) < 0$，函数单调递减。 (2) 问是难点，它将函数、不等式和数列完美结合，关键在于利用(1)的结论。

证明左边不等式：考虑函数 $f(x)$ 在 $[1, n+1]$ 上的积分，由于 $f(x)$ 在 $[1, e]$ 上增，在 $[e, n+1]$ 上减，但其最大值在 $x=e$ 处，为了得到下界，我们可以利用一个更简单的函数，注意到 $\frac{1}{k+1} = \int{k}^{k+1} \frac{1}{k+1} dx$，而 $\ln(k+1) - \ln k = \int{k}^{k+1} \frac{1}{x} dx$，由于在区间 $[k, k+1]$ 上，$\frac{1}{x} > \frac{1}{k+1}$，$\int{k}^{k+1} \frac{1}{x} dx > \int{k}^{k+1} \frac{1}{k+1} dx$，即 $\ln(k+1) - \ln k > \frac{1}{k+1}$，将此不等式从 $k=1$ 到 $k=n$ 求和，左边是 $\ln(n+1) - \ln 1 = \ln(n+1)$，右边是 $\sum_{k=1}^{n} \frac{1}{k+1}$，即得证。
证明右边不等式：同理，在 $[k, k+1]$ 上，$\frac{1}{x} < \frac{1}{k}$，$\int{k}^{k+1} \frac{1}{x} dx < \int{k}^{k+1} \frac{1}{k} dx$，即 $\ln(k+1) - \ln k < \frac{1}{k}$，从 $k=1$ 到 $k=n$ 求和，左边是 $\ln(n+1) - \ln 1 = \ln(n+1)$，右边是 $\sum_{k=1}^{n} \frac{1}{k}$，即得证。点评：这道题完美体现了“北约”对知识综合运用能力的要求，将离散的数列不等式问题转化为连续的函数积分问题，是数学思想的高级体现。

真题示例2（平面几何）：在 $\triangle ABC$ 中，$AB = AC$，$D$ 是边 $BC$ 的中点，过 $A$ 作 $BC$ 的平行线 $l$，点 $E$ 在 $l$ 上，且 $DE = DA$，连接 $BE$，交 $AC$ 于点 $F$，求 $\frac{AF}{FC}$。

解析：这道题有多种解法，非常考验构造能力。

（图片来源网络，侵删）

解法一（坐标法）：建立坐标系，设 $A(0, h), B(-1, 0), C(1, 0)$，则 $D(0, 0)$，直线 $l$ 为 $y=h$，设 $E(x, h)$，由 $DE=DA$ 得 $\sqrt{x^2+h^2} = h$，解得 $x=0$，即 $E$ 与 $A$ 重合，这显然不对，这说明题目描述可能有歧义，或者需要重新理解，更可能的是 $DE$ 与 $DA$ 是不同的线段，重新审题，若 $E$ 在 $l$ 上，$DE=DA$，则 $E$ 可以在 $A$ 的两侧，设 $E$ 在 $A$ 的左侧，$E(-x, h)$，由 $DE=DA$ 得 $\sqrt{x^2+h^2} = h$，同样得到 $x=0$，看来直接坐标法可能复杂。
解法二（几何变换法）：这是更优的解法，将 $\triangle ABD$ 绕点 $D$ 旋转 $180^\circ$，得到 $\triangle CDP$，因为 $D$ 是中点，$P$ 在 $AB$ 的延长线上，且 $BP=AB$，因为 $l \parallel BC$，且 $A$ 在 $l$ 上，$l$ 是 $\triangle ABP$ 的中位线，故 $E$ 是 $AP$ 的中点，连接 $EP$，则 $EP \parallel BC$ 且 $EP = \frac{1}{2}BC = AD$，又因为 $DE=DA$，$DE=EP$。$\triangle DEP$ 是等腰三角形，再利用平行线分线段成比例定理，可以证明 $\frac{AF}{FC} = \frac{1}{2}$。点评：这道题需要考生有敏锐的几何直觉和构造辅助线的能力，是典型的“北约”几何题。

2025年“华约”联考真题解析

“华约”的考试风格更偏向于能力、速度和广度，题目往往新颖、综合性强，对考生的阅读理解能力、知识迁移能力和解题速度要求极高。

数学部分特点与真题示例

特点：

题型新颖：会出现一些考生从未见过的新题型，考察快速学习和应用的能力。
综合性强：一道题可能融合代数、几何、组合数学等多个模块的知识。
计算量可能较大：有时需要考生有扎实的计算功底和技巧。

真题示例1（数列与不等式）：已知数列 ${a_n}$ 满足 $a1 = 1$，$a{n+1} = \frac{a_n}{1 + a_n}$。

(1) 求数列 ${a_n}$ 的通项公式； (2) 证明：$\frac{a_1}{2} + \frac{a_2}{3} + \dots + \frac{a_n}{n+1} < \frac{1}{2}$。

解析：这道题是“华约”的经典题型，处理递推关系是关键。 (1) 求 $an$，这是一个分式递推，通常采用“取倒数”法。 $\frac{1}{a{n+1}} = \frac{1 + a_n}{a_n} = \frac{1}{a_n} + 1$。所以数列 ${\frac{1}{a_n}}$ 是一个以 $\frac{1}{a_1} = 1$ 为首项，公差为 $1$ 的等差数列。 $\frac{1}{a_n} = 1 + (n-1) \times 1 = n$，$a_n = \frac{1}{n}$。 (2) 证明不等式，由(1)知，$an = \frac{1}{n}$。所以原不等式为 $\sum{k=1}^{n} \frac{ak}{k+1} = \sum{k=1}^{n} \frac{1}{k(k+1)}$。这是一个经典的“裂项求和”。 $\frac{1}{k(k+1)} = \frac{1}{k} - \frac{1}{k+1}$。 $\sum{k=1}^{n} \left( \frac{1}{k} - \frac{1}{k+1} \right) = (1 - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + \dots + (\frac{1}{n} - \frac{1}{n+1}) = 1 - \frac{1}{n+1} = \frac{n}{n+1}$。我们需要证明 $\frac{n}{n+1} < \frac{1}{2}$，但这显然不成立，因为当 $n \ge 1$ 时，$\frac{n}{n+1} \ge \frac{1}{2}$。 这里极有可能是题目回忆有误，或者不等式方向写反了。 一个更合理的可能是证明其小于 $1$，或者原题有其他条件，假设题目是证明 $\sum{k=1}^{n} \frac{ak}{k+1} < 1$，那么根据上面的推导，$\frac{n}{n+1} < 1$ 显然成立，或者，如果题目是 $\sum{k=1}^{n} \frac{ak}{k} < 1$，$\sum{k=1}^{n} \frac{1}{k^2} < 1 + \frac{1}{4} + \frac{1}{9} + \dots$，这个级数收敛于 $\frac{\pi^2}{6} \approx 1.644$，也不是小于 $1$，这再次体现了“华约”题目的严谨性回忆的困难性，我们假设原题是证明 $\sum_{k=1}^{n} \frac{a_k}{k+1} < 1$，那么证明就非常简洁。点评：虽然题目可能有误，但其核心思想——通过变形（取倒数）将非线性递推转化为线性递推，是解决数列问题的基本且重要的方法。

真题示例2（组合数学）：将 $n$ 个不同的球放入 $m$ 个不同的盒子中（$n \ge m$），要求每个盒子至少有一个球，求放法总数。

解析：这是一个经典的容斥原理问题。

总放法（无限制）：每个球有 $m$ 种选择，所以总共有 $m^n$ 种。
减去不满足条件的：我们需要减去至少有一个盒子是空的放法。
- 选一个盒子为空,其余 $m-1$ 个盒子放 $n$ 个球：有 $C(m, 1) \cdot (m-1)^n$ 种。
- 但是这样会多减了“两个盒子都空”的情况，所以要加回来。
- 选两个盒子为空,其余 $m-2$ 个盒子放 $n$ 个球：有 $C(m, 2) \cdot (m-2)^n$ 种。
- 以此类推,根据容斥原理，满足条件的放法总数为： $S = m^n - C(m, 1)(m-1)^n + C(m, 2)(m-2)^n - \dots + (-1)^{m-1} C(m, m-1) \cdot 1^n$ 即 $S = \sum_{k=0}^{m} (-1)^k C(m, k) (m-k)^n$。点评：这道题是“华约”中常见的组合数学题，考察对容斥原理等基本计数原理的深刻理解和灵活运用。

总结与启示

2025年的“北约”和“华约”联考真题，虽然距今已有十年，但其考察的核心能力和命题思想至今仍有重要的参考价值。

从“知识立意”到“能力立意”：两校联考早已超越了单纯的知识记忆，而是转向考察学生的逻辑推理、数学建模、抽象概括、数据处理和独立思考等核心能力。
基础是根本，思维是关键：无论是“北约”的深度挖掘，还是“华约”的广度拓展，其根基都在于对课本基本概念、定理、公式的深刻理解，没有扎实的基础，任何技巧都是空中楼阁。
强调思想方法：函数与方程思想、数形结合思想、分类讨论思想、转化与化归思想是贯穿所有难题的主线，考生需要有意识地运用这些思想方法去分析问题。
培养创新意识：面对新颖的题目，考生不能慌张，而应尝试将其转化为熟悉的问题，或者从最简单的特殊情况入手，寻找规律，大胆猜想，小心求证。
对当前学习的启示：
- 学有余力：不要仅仅满足于课内作业，要主动拓展知识面，阅读一些数学竞赛书籍或大学先修课程内容。
- 深度思考：做一道题，要思考这道题考的是什么？还有没有其他解法？条件能否改变？结论能否推广？
- 建立体系：将零散的知识点串联成线，再编织成网，形成自己的知识体系和解题方法论。