这是一个非常常见的问题,关于首都师范大学的音乐学院,答案是:它是一本院校,并且其音乐专业在全国范围内享有很高的声誉。
(图片来源网络,侵删)
为了给您一个更清晰、更全面的解释,我们可以从以下几个层面来理解:
从录取批次来看(“几本”的原始含义)
在中国高考招生体系中,“一本”、“二本”是指录取的批次,随着高考改革的推进,很多省份已经合并了本科批次,不再明确区分“一本”和“二本”,但即便在还区分批次的省份,首都师范大学也绝对是“一本”院校。
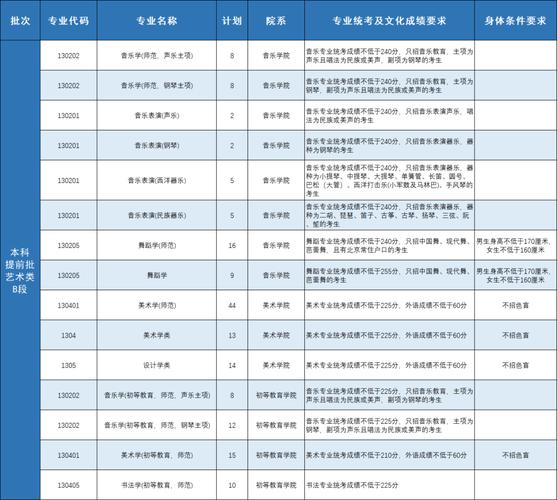
- 北京市:首都师范大学是北京市属重点大学,在北京市的招生中,其所有专业(包括音乐学院)都在本科提前批或本科一批次进行招生,录取分数线远高于一本线。
- 其他省份:在全国绝大多数省份,首都师范大学都是在本科第一批次(一本批次)进行招生的,这意味着,能被首都师范大学录取的学生,通常都是所在省份成绩非常优秀的学生。
从学校综合实力来看
首都师范大学本身就是北京市重点建设大学,是国家“双一流”建设高校,学校的整体定位就是一所高水平的综合性师范大学,在全国师范类院校中名列前茅,它的下属学院,尤其是像音乐学院这样的优势学院,自然也是高起点、高水平的。
从音乐学院的专业实力来看(这是最核心的一点)
对于艺术生来说,学校的“几本”标签远不如其专业实力和行业认可度重要,首都师范大学音乐学院在这方面非常出色:

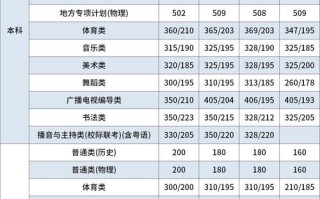
(图片来源网络,侵删)
- 历史悠久,底蕴深厚:学院创建于1964年,是北京市最早建立的高等音乐教育机构之一,拥有悠久的历史和深厚的文化底蕴。
- 名师荟萃,师资力量强大:学院拥有一支由国内外知名音乐家、学者和教育家组成的教师队伍,教学和科研实力雄厚。
- 学科齐全,专业优势突出:学院设有音乐学、作曲与作曲技术理论、音乐表演、录音艺术等多个专业方向,其中音乐学是国家级重点学科,这是非常高的荣誉。
- 平台广阔,实践机会多:地处北京,学院学生有更多机会参与国家级的艺术活动、演出和比赛,与国内外顶尖艺术团体和院校交流合作。
- 就业前景好:毕业生遍布全国各地的中小学、高等院校、文艺团体、研究机构和媒体行业,培养了大量优秀的音乐教育人才和表演人才,在行业内口碑很好。
- 从招生批次上讲:首都师范大学是一本院校,音乐学院自然也是一本招生。
- 从专业实力上讲:首都师范大学音乐学院是全国顶尖的音乐学院之一,其专业水平和社会认可度远超“一本”这个标签所能概括的范畴,对于有志于从事音乐学习和工作的学生来说,这是一个非常值得报考的顶尖选择。
当别人问起时,您最准确、最全面的回答应该是:首都师范大学是一本大学,它的音乐学院是国家级重点学科,专业实力非常强,在全国都很有名。
(图片来源网络,侵删)
标签: 首都师范大学音乐学院是一本吗 首都师范大学音乐学院录取分数线 首都师范大学音乐学院怎么样
版权声明:除非特别标注,否则均为本站原创文章,转载时请以链接形式注明文章出处。