这是一个非常好的问题,但答案并不是一个固定的数字,因为它取决于多个关键因素,舞蹈专业上一本线的分数没有一个“全国统一标准”,而是由以下几个变量共同决定的:
(图片来源网络,侵删)
核心影响因素
招生类型:这是最关键的区别!
舞蹈专业的招生主要分为两大类,它们的录取规则完全不同:
-
艺术类(校考/联考)招生
- 这是绝大多数舞蹈专业学生的主要途径。
- 录取规则:高考文化课成绩 专业课成绩(省统考/联考成绩或校考合格证),按照一定的比例折算成综合分,从高到低录取。
- 分数线构成:
- 专业课线:首先要通过你所在省份的舞蹈类专业省统考(联考),拿到合格证,部分顶尖院校(如北京舞蹈学院、中央民族大学等)还会组织校考,需要拿到他们的专业合格证。
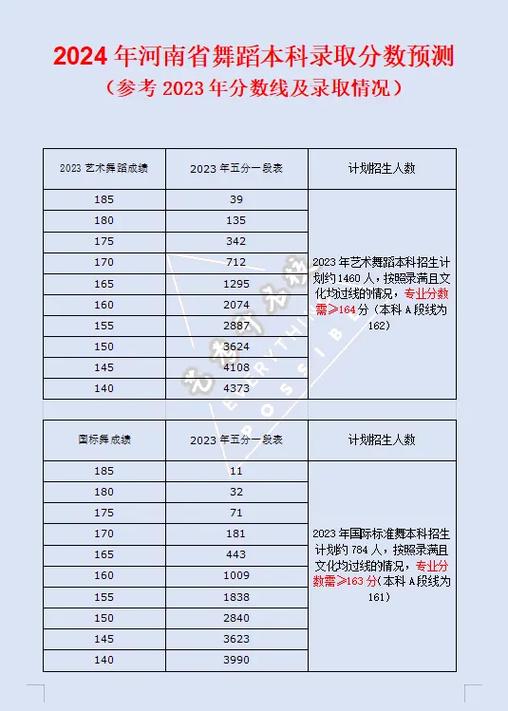
- 文化课线:在专业课合格的基础上,你的高考文化课成绩必须达到艺术类专业的最低控制分数线(俗称“艺术线”或“省控线”),这个分数线通常远低于普通一本线(特控线)。
- 对于这类招生,不存在一个“一本文化分”,你不需要达到普通理科/文科的一本线,而是要达到艺术类的文化分线,并且在专业上足够优秀。
-
普通类(文化课)招生
- 这类情况非常非常少,仅存在于极少数综合性大学的舞蹈学专业,并且通常对文化课要求极高。
- 录取规则:完全按照高考文化课成绩,从高到低择优录取,和填报普通文理志愿一样。
- 分数线:这类专业的录取分数线通常就是普通类的一本线(特控线)甚至更高。
- 如果你报考的是这类专业,那么你的文化分就需要达到一本线。
所在省份
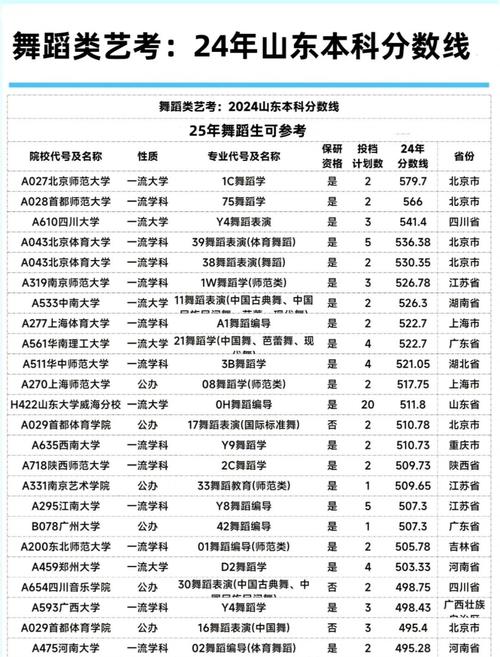
- 不同省份的教育水平、考生人数、招生计划都不同,因此舞蹈专业的省控线、各院校的录取分数线差异很大,北京、山东、河南等省份的竞争激烈程度和分数线就远高于其他地区。
目标院校
- 顶尖艺术院校:如北京舞蹈学院、中央民族大学、上海戏剧学院等,这些学校对专业要求极高,竞争极其激烈,即使它们的录取规则是综合分,但专业分占的比重通常很大,且文化分要求也在逐年提高,很多热门专业的实际录取综合分远超一本线。
- 重点综合性大学:如北京师范大学、华中师范大学、南京师范大学等,这类学校的舞蹈学专业对文化课要求通常比纯艺术院校更高,综合分计算时文化课占比可能更大。
- 普通一本院校:如各省的师范大学、综合大学等,分数线相对会低一些,但依然是按综合分从高到低录取。
如何查询准确的分数线?
既然没有固定答案,那么最准确的方法就是“查询目标院校近三年的招生简章和录取数据”,具体步骤如下:
(图片来源网络,侵删)
- 确定目标院校和专业:你想考哪些学校?哪个学校的舞蹈专业?
- 访问学校招生网:进入目标院校的“本科招生网”或“招生办公室”官网。
- 查找招生简章:找到最近三年的《艺术类专业招生简章》,这是最重要的文件!
- 关注关键信息:
- 招生省份:该专业在你所在省份是否招生?
- 录取规则:是“文化课过线,按专业分排序”还是“综合分录取”?如果是综合分,文化课和专业课的比例是多少?(文化课占40%,专业课占60%)
- 录取分数线:官网通常会公布最近几年的各专业录取最低分(可能是综合分,也可能是文化分和专业分),这是你最重要的参考依据。
总结与建议
| 招生类型 | 录取规则 | 文化课要求 | |
|---|---|---|---|
| 艺术类(校考/联考) | 综合分 = 文化分 × 权重 + 专业分 × 权重 | 只需达到艺术类省控线(远低于一本线) | 这是主流方式,关键看综合分排名,专业能力是核心。 |
| 普通类(文化课) | 按高考文化分从高到低录取 | 通常需要达到或超过普通一本线(特控线) | 极少见,对文化课要求极高,适合文化成绩特别好的学生。 |
给你的建议:
- 明确方向:先确定你想走哪条路,99%的舞蹈生走的是第一条路(艺术类招生)。
- 两手准备:专业和文化课都不能丢,专业要争取在省统考/校考中取得高分,这是你的敲门砖,文化课要努力达到甚至超过艺术类省控线,在综合分计算中占据优势。
- 精准定位:根据自己的专业水平和文化课成绩,圈定几所不同层次的院校(冲刺、稳妥、保底),然后去查询这些学校近三年的具体录取数据,制定一个现实的分数目标。
- 关注趋势:近年来,教育部越来越强调文化素养,各大艺术类院校对舞蹈专业考生的文化课要求普遍在逐年提高,所以一定要重视文化课的学习。
希望这个详细的解释能帮助你更好地规划备考!祝你成功!
(图片来源网络,侵删)
标签: 舞蹈专业一本录取分数线查询 舞蹈一本院校录取分数线要求 舞蹈专业一本文化课分数线多少
版权声明:除非特别标注,否则均为本站原创文章,转载时请以链接形式注明文章出处。






